Resumen
En este estudio se modelan los rendimientos cambiarios de diez países asiáticos y latinoamericanos usando los modelos autor-regresivos con heteroscedasticidad condicional GARCH, TGARCH y EGARCH. Los resultados principales indican que los shocks informacionales tienen efectos simétricos sobre la volatilidad de los rendimientos cambiarios de Chile. En Brasil, China, Colombia, Corea del Sur, Malasia y México las malas noticias incrementan la volatilidad en los rendimientos cambiarios. Finalmente, se muestra que el modelo AR(1)-TGARCH(1,1) y la distribución GED explican de manera adecuada la mayoría de las series de rendimientos cambiarios.
Abstract
In this study, we model the exchange-rate returns of ten Asian and Latin-American countries using the GARCH, TGARCH and EGARCH autoregressive conditional heteroskedasticity models. The main results show that informational shocks have symmetric effects on the volatility of the Chilean exchange-rate returns. In Brazil, China, Colombia, South Korea, Malaysia and Mexico, bad news increase the volatility of exchange-rate returns. Finally, we show that the AR(1)-TGARCH(1,1) model and the GED distribution describe in an adequate manner most of the series of exchange-rate returns.
INTRODUCCIÓN
Uno de los mercados con mayor relevancia en el mundo es el mercado cambiario. La importancia del mercado de divisas es que permite determinar el precio de una moneda en términos de otra. Las transacciones que se realizan dentro del mercado de divisas son la referencia para el resto de los mercados financieros internacionales (Diez de Castro y Medrano, 2007). El principal interés del tipo de cambio radica en la importancia que tiene sobre la estabilidad macroeconómica de los países y en la relación con otras variables fundamentales. Siguiendo a Fullerton, Hattori y Calderón (2001), la volatilidad que provocan los tipos de cambio puede tener efectos en los niveles de precios, la tasa de interés e incluso en la balanza comercial.
En esta investigación se estudia la pertinencia de modelar las series de los rendimientos cambiarios a corto plazo. La investigación se justifica porque se argumenta que las formas bajo las cuales los agentes anticipan el valor futuro de las monedas y el impacto que causan las noticias sobre el tipo de cambio son muy complejas de modelar (Vitale, 2007). La modelación de los rendimientos cambiarios propuesta aquí utiliza modelos de los tipos GARCH, TGARCH y EGARCH. El primer tipo de modelo es simétrico, mientras que los siguientes dos son modelos asimétricos. Esto significa que mientras en el primer modelo se asume que las buenas y malas noticias tienen efectos de magnitud similar, pero de signo contrario, sobre los rendimientos cambiarios; en los últimos modelos se asume que los efectos tienen magnitudes diferentes. Particularmente, los tipos de cambio analizados son los de diez economías emergentes de Asia y Latinoamérica.
Académicamente, ésta investigación complementa la literatura sobre la modelación de los rendimientos cambiarios para países emergentes de Asia y Latinoamérica. Particularmente, se aporta evidencia para analizar la conveniencia de utilizar supuestos informacionales de asimetría sobre la volatilidad de los rendimientos cambiarios. Asimismo, se modelan las perturbaciones usando la distribución generalizada de los errores (GED, por sus siglas en inglés). La mayoría de los trabajos usan distribuciones normales o t de Student.
El estudio está organizado en siete secciones, incluida ésta parte introductoria y la conclusión. El orden es el siguiente: la sección 1 revisa la literatura; la sección 2 describe la metodología empleada y los modelos GARCH, TGARCH y EGARCH; la sección 3 presenta la base de datos y el análisis de estadística descriptiva de las series de los rendimientos cambiarios; la sección 4 presenta el análisis de estacionariedad de las series de los tipos de cambio; la sección 5 muestra la modelación econométrica y los resultados de las estimaciones y la última sección sintetiza las conclusiones y los resultados.
1. REVISIÓN DE LA LITERATURA
Los modelos auto-regresivos con heteroscedasticidad condicional (Auto-Regressive Conditional Heteroskedasticity, ARCH) se han utilizado para describir y pronosticar el comportamiento y volatilidad de las series de rendimientos cambiarios. Si bien su uso es frecuente en los países desarrollados, los estudios que los usan para modelar los rendimientos latinoamericanos son escasos. Particularmente, Ruiz (2009) analiza los rendimientos cambiarios de trece países latinoamericanos usando modelos ARCH de factores comunes de dos variables. Los resultados indican que la mayoría de las monedas tienen varianza variable en el tiempo. Martínez y Ramírez (2011) analizan los tipos de cambio de Brasil, Chile, Colombia, México y Perú con modelos multivariados dinámicos. Los estudios aquí mencionados usan modelos simétricos, es decir, que asumen que las buenas y malas noticias tienen el mismo impacto sobre la volatilidad de los rendimientos.
En la literatura hay quienes sustentan que las volatilidades de los rendimientos cambiarios experimentan asimetrías en la presencia de buenas y malas noticias (McKenzie, 2002). Particularmente, entre quienes suponen la existencia de asimetrías se encuentra Fernández (2005), quien usa tres modelos GARCH asimétricos para describir los rendimientos del peso chileno/dólar. Maya y Gómez (2008), por su parte, analizan los rendimientos cambiarios de Brasil, Chile, Colombia, México y Perú mediante modelos HYPARCH. Castaño, Gómez y Gallón (2008) realizan un análisis del comportamiento de los rendimientos del peso colombiano/dólar utilizando un modelo HYAPGARCH y un IGARCH. Lorenzo y Ruíz (2012) analizan las dinámicas de corto y largo plazo en los rendimientos cambiarios de Argentina, Brasil, Chile, Colombia, México y Perú usando modelos TGARCH y EGARCH. Ellos encuentran evidencia de que en el corto plazo en la mayoría de los países analizados, las buenas y malas noticias tienen un impacto simétrico.
Los modelos de la familia ARCH también se han usado para modelar las series de rendimientos cambiarios de algunos países asiáticos. Así, Dias y Embrechts (2010) utilizan un modelo GARCH-cópula variable en el tiempo para describir los rendimientos del yen/dólar. Cai, Chen y Fang (2010) analizan el tipo de cambio dólar/yuan mediante un modelo con coeficientes funcionales y un modelo GARCH. Jebran y Iqbal (2016) estudian los efectos de contagio entre las volatilidades de los mercados de divisas y de valores en Pakistán, India, Sri Lanka, China, Hong Kong y Japón mediante un EGARCH bidireccional. Sus resultados sugieren que la volatilidad del mercado de valores se transmite de manera unidireccional hacia el mercado de divisas. Finalmente, Choi (2016) analiza la volatilidad entre los tipos de cambio won/dólar y el won/yen mediante modelos GARCH y TGARCH. Sus resultados indican que existen efectos ARCH en los tipos de cambio y que la volatilidad del tipos de cambio won /dólar es más grande que la correspondiente al won/yen.
2. METODOLOGÍA DE ANÁLISIS
Los datos usados en esta investigación contemplan los tipos de cambio diarios de diez países1, donde cinco son países asiáticos y los otros cinco países latinoamericanos. El análisis se hace para el periodo comprendido del 05 de agosto de 2002 al 22 de enero de 2016. Se usan los precios de cierre diarios, excluyendo los fines de semana y los días festivos. Por convención, los valores de los tipos de cambio se expresan en términos de logaritmos naturales. Una vez teniendo los logaritmos naturales se crean las series que expresan los rendimientos de los tipos de cambio. Así, el logaritmo natural del tipo de cambio del país i en el día t, se define como ln Pit, El rendimiento cambiario del país i en el día t, rit, se define como la diferencia de los logaritmos:
Las técnicas de análisis utilizadas en esta investigación consisten en: análisis de la estadística descriptiva, correlaciones pairwise, análisis de estacionariedad y modelos GARCH, TGARCH y EGARCH univariados. La estadística descriptiva se utiliza para describir las características de las series de los rendimientos cambiarios. Los análisis pairwise se usan para analizas las relaciones entre las series. El análisis de la estacionariedad se utiliza para analizar la pertinencia de modelar las series cambiarias. Los modelos GARCH, TGARCH y EGARCH se usan para modelar simultáneamente las medias y varianzas de las series de los rendimientos cambiarios.
El modelo GARCH, propuesto por Bollerslev (1987), es una generalización de los modelos ARCH. Particularmente, la especificación del modelo AR(1)-GARCH(1,1) usado aquí es:
La especificación del modelo AR(1)-GARCH(1,1) debe cumplir que los parámetros 
, 
y 
sean positivos y que 
(condición de estacionariedad). Si bien la distribución condicional de 
es la GED, debe señalarse que 
debe comportarse como ruido blanco (white noise). En el modelo GARCH tanto las buenas como las malas noticias tienen el mismo impacto, es decir, tienen un efecto simétrico.
El modelo TGARCH, propuesto por Zakoian (1994), se usa aquí para considerar la potencial existencia de efectos informacionales asimétricos. Se usa éste modelo en virtud de que, de acuerdo con Gabriel (2012) y Lim y Seck (2013), el mismo es el más adecuado para explicar los rendimientos de los mercados emergentes. Particularmente, aquí se usa la especificación del modelo AR(1)-TGARCH (1,1):
La especificación del modelo AR(1)-TGARCH(1,1) hace que el efecto de la volatilidad asociada a un impacto positivo (buenas noticias), 
sea 
. El efecto asociado a un impacto negativo (malas noticias), es 
. Las perturbaciones sobre la volatilidad son asimétricas porque que el parámetro, 
afecta la varianza condicional solo cuando las noticias en el mercado son malas . Además, si 
, ocurre el llamado “efecto apalancamiento” (i.e., las malas noticias incrementan la volatilidad en los rendimientos cambiarios).
Finalmente, el tercer modelo es una variación del EGARCH desarrollado por Nelson (1991). El modelo EGARCH permite la existencia de asimetrías entre los rendimientos y la volatilidad mediante una forma funcional logarítmica. Para efectos del estudio, el modelo AR(1)-EGARCH (1,1) está dado por la siguiente especificación:
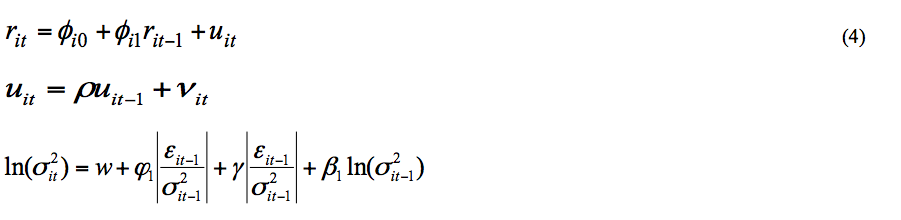
En la especificación del modelo AR(1)-EGARCH(1,1), el parámetro g modela la asimetría. Sin embargo, la interpretación del signo del parámetro es opuesta a su contraparte del modelo TGARCH. Por tanto, si 
, ocurre el llamado “efecto apalancamiento”. Otra característica de éste modelo es que la varianza nunca puede ser negativa.
Finalmente, el análisis econométrico de los modelos GARCH, TGARCH y EGARCH se sustenta en pruebas de significancia individual y en la bondad de ajuste de los modelos. Las pruebas de significancia se evalúan mediante los p-values asociados a los estadísticos z de los coeficientes. La bondad de ajuste se estima con base en estimaciones del Logaritmo de Verosimilitud (Logl) y el Criterio de Información de Akaike (AIC). Las estimaciones mencionadas se usan para determinar el modelo que mejor describe los rendimientos cambiarios de los países analizados.
3. BASE DE DATOS Y RENDIMIENTOS CAMBIARIOS ASIÁTICOS Y LATINOAMERICANOS
La base de datos se obtiene de la plataforma Investing2. La misma comprende diez series de tipos de cambio. Cada serie incluye 3.744 observaciones diarias. Las mismas se utilizan para construir las diez series de rendimientos diarios con base en la ecuación (1).
La tabla 1 muestra que todas las series de rendimientos cambiarios tienen curtosis muy elevadas, por lo que son leptocúrticas. Las curtosis estimadas son mayores a 3, salvo para el caso de los rendimientos de Argentina. El sesgo, también conocido como coeficiente de asimetría, es positivo para tres series y negativo para las restantes. Las desviaciones estándar estimadas sugieren la existencia de volatilidades no constantes. Además, los estadísticos Jarque-Bera y sus respectivos p-values, muestran que ninguna de las series se distribuye de manera normal.
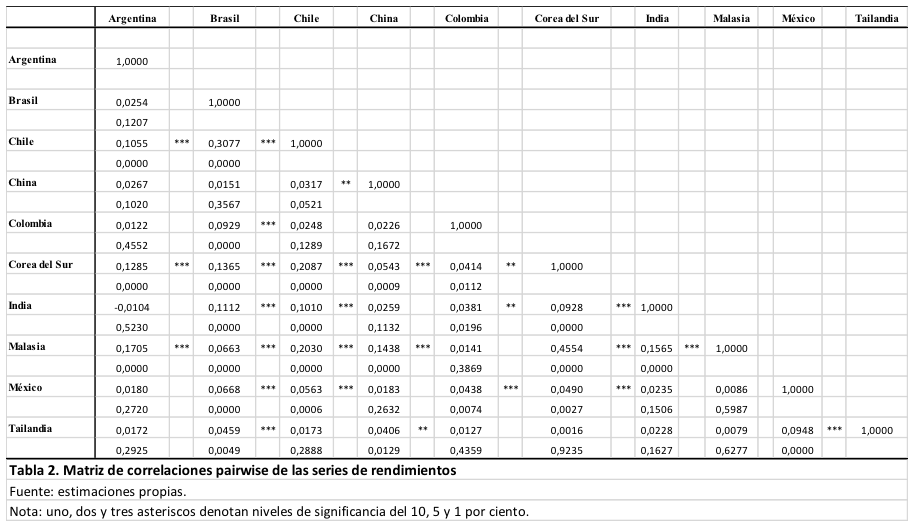
La tabla 2 reporta la matriz de correlaciones pairwise de los rendimientos cambiarios. Los resultados indican que la mayoría de los rendimientos están correlacionados positivamente. Lo anterior sugiere que si el tipo de cambio se aprecia en un país, entonces ocurrirá lo mismo en los demás países.
4. ANÁLISIS DE ESTACIONARIEDAD
El análisis de estacionariedad se utiliza para evaluar la conveniencia de modelar las series cambiarias. Para el presente trabajo se utiliza la prueba de Phillips-Perron (PP) para evaluar el orden de integración de las series de rendimientos cambiarios de cada uno de los países analizados. Estadísticamente, el uso de éste test se justifica porque permite evaluar la existencia de raíces unitarias y de regresiones potencialmente espurias.
La tabla 3 muestra que los tipos de cambio expresados en términos de logaritmos son integrados de orden uno I(1). Esto significa que las series de rendimientos cambiarios son estacionarias. Asimismo, implica que las series de los rendimientos cambiarios son susceptibles de ser descritas y analizadas mediante los modelos GARCH, TGARCH y EGARCH. La estimación de los modelos no conllevaría la estimación de regresiones espurias.
5. ANÁLISIS ECONOMÉTRICO DE MODELACIÓN
En esta sección se estiman los modelos propuestos. Además, se incluye la prueba de efectos ARCH-LM para analizar la conveniencia de describir los rendimientos mediante dichos modelos. La hipótesis nula de la prueba plantea que no existe heteroscedasticidad condicional en los residuales. Por tanto, su rechazo implica que las series pueden ser descritas y analizadas mediante modelos de la familia ARCH.
La tabla 4 muestra que la mayoría de las series de rendimientos pueden ser descritas mediante los modelos de la familia ARCH. Solo los rendimientos de Argentina no pueden describirse mediante dichos modelos debido a que sus residuales no presentan heteroscedasticidad condicional. Así, la evidencia muestra que las series de rendimientos cambiarios de los cinco países asiáticos y de cuatro países latinoamericanos son susceptibles a ser modelados estadísticamente mediante los modelos GARCH, TGARCH y EGARCH.
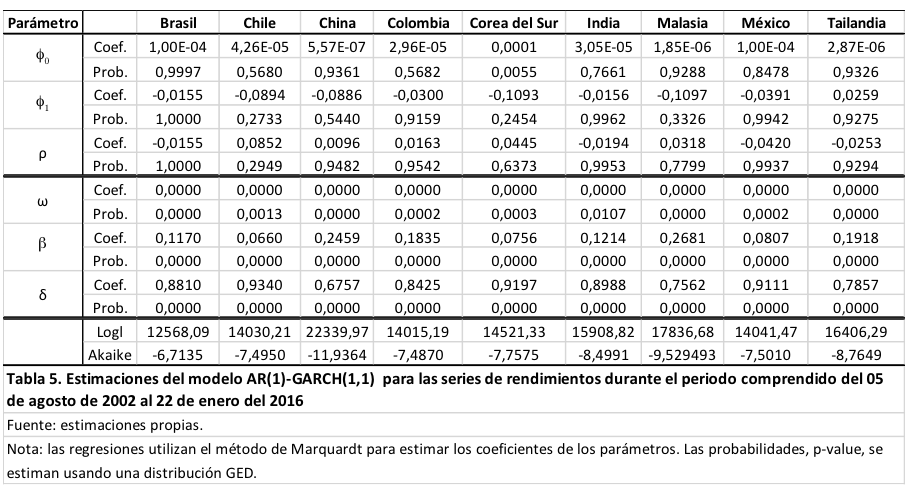
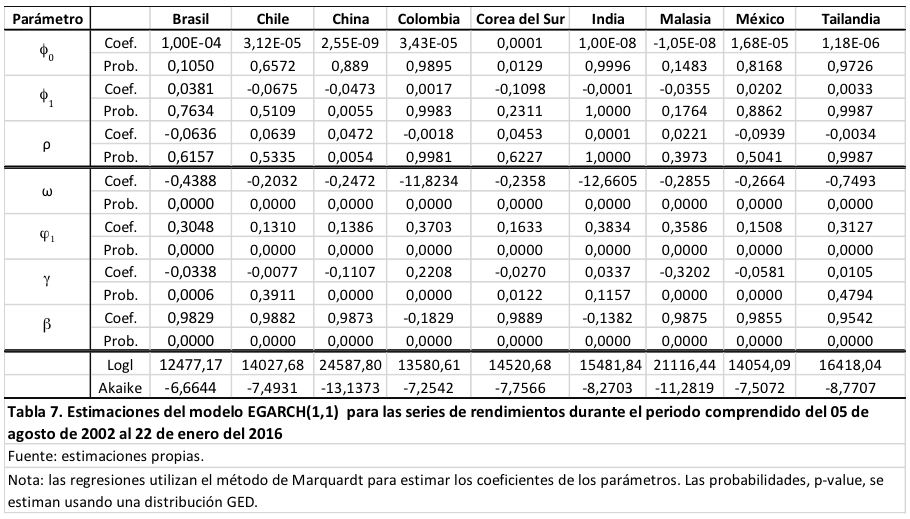
Las tablas 5, 6 y 7 muestran las estimaciones de los modelos GARCH, TGARCH y EGARCH usados para describir a las series de los rendimientos cambiarios. La mayoría de las estimaciones de los parámetros se obtienen usando el algoritmo Marquardt. La excepción se refiere a la estimación del modelo EGARCH usado para describir los rendimientos de Brasil. Para este último país, las estimaciones se obtienen usando el algoritmo Berndt-Hall-Hall-Hausman (BHHH).
La tabla 8 reporta las estimaciones de bondad de ajuste para los modelos estimados. Particularmente, los resultados indican que el modelo que mejor describe los rendimientos cambiarios de Chile es el AR(1)-GARCH(1,1). Las estimaciones muestran que los rendimientos cambiarios de Brasil, Colombia, Corea del Sur, India y México se describen mejor mediante el modelo AR(1)-TGARCH(1,1). Finalmente, las estimaciones muestran que los rendimientos de los tipos de cambio de China, Malasia y Tailandia pueden ser descritos de manera adecuada mediante el modelo AR(1)-EGARCH(1,1).
Econométricamente, los resultados de las estimaciones de bondad de ajuste de la tabla 8 pueden combinarse con los resultados de las tablas 5, 6 y 7. Particularmente, las tablas 5 y 8 muestran que las buenas y las malas noticias tienen el mismo impacto sobre la volatilidad de los rendimientos cambiarios de Chile. Así los resultados sugieren que los inversores en pesos chilenos son relativamente neutrales al riesgo. Las tablas 6 y 8 muestran que los rendimientos cambiarios manifiestan “efectos apalancamiento” significativos en Brasil, Colombia, Corea del Sur y México. Asimismo, proveen evidencia no significativa de que pudieran manifestarse en los rendimientos de la India. Finalmente, las tablas 7 y 8 muestran que los rendimientos cambiarios manifiestan “efectos apalancamiento” significativos en China y Malasia. Asimismo, proveen evidencia no significativa de que las malas noticias reducen la volatilidad de los rendimientos cambiarios de Tailandia.
CONCLUSIONES Y DISCUSIÓN
En este trabajo se ha desarrollado un análisis econométrico de los rendimientos cambiarios de países asiáticos y latinoamericanos usando modelos GARCH, EGARCH y TGARCH univariados. El uso de estos tres modelos ha permitido analizar los efectos de shocks informacionales sobre la volatilidad de los rendimientos cambiarios. La modelación de los rendimientos mediante los mencionados modelos se justifica en términos de los análisis estadísticos utilizados.
Los principales resultados del trabajo son los siguientes: (1) la evidencia sugiere que los shocks informacionales tienen efectos simétricos sobre la volatilidad de los rendimientos cambiarios de Chile; (2) en Brasil, China, Colombia, Corea del Sur, Malasia y México, las malas noticias incrementan la volatilidad de los rendimientos cambiarios; (3) las dinámicas de corto plazo de los rendimientos son descritas por los modelos AR(1)-GARCH(1,1), AR(1)-EGARCH(1,1) y el AR(1)-TGARCH(1,1) para un total de 1, 3 y 5 países, respectivamente; y (4) el modelo AR(1)-TGARCH(1,1) y la distribución GED explican de manera adecuada la mayoría de las series de rendimientos cambiarios.
La modelación de las series cambiarias y el análisis de los shocks informacionales son de suma importancia para la econometría financiera y para la formulación de políticas económicas y financieras. Además, siguiendo a Frankel y Froot (1990), es relevante determinar si el tipo de cambio está valuado correctamente ya que ésta variable afecta simultáneamente a los precios de los activos extranjeros, a los precios de los bienes nacionales y a los precios de los factores de producción.
De esta manera, se deja abierta la posibilidad de realizar investigaciones futuras que permitan discutir y analizar los mercados cambiarios de países emergentes.
REFERENCIAS
[1] Bollerslev, T. (1987). “A Conditional Heteroskedastic Time Series Model for Speculative Prices and Rates of Return”. Review of Economics and Statistics, 69(3), pp. 542-547.
[2] Cai, Z.; Chen, L. y Fang, Y. (2010). “A New Forecasting Model for USD/CNY Exchange Rate.” Studies in Nonlinear Dynamics and Econometrics, 16(3), pp. 1558-3708.
[3] Castaño, E; Gómez, K. y Gallón, S. (2008). “Pronóstico y estructuras de volatilidad multiperíodo de la tasa de cambio del peso colombiano”. Cuadernos de Economía, 48, pp. 241-266.
[4] Choi, J. E. (2016). “A Study on the Comparative Analysis of Volatility between Won-Dollar Exchange Rates and Won-Yen Exchange Rates According to the Mutation of Financial Environments.” Full Paper Proceeding BESSH, 76(3), pp. 15-23.
[5] Dias, A. y Embrechts, P. (2010). “Modeling Exchange Rate Dependence Dynamics at Different Time Horizons”. Journal of International Money and Finance, 29(8), pp. 1687-1705.
[6] Diez de Castro, L. T. y Medrano, M. L. (2007). Tipos de cambio. En: Mercados Financieros Internacionales (pp. 25-38). Madrid, España: Dykinson.
[7] Fernández, V. (2005). How Sensitive is Volatility to Exchange Rate Regimes? En: Arbelaez H. y Click R.W. (Eds). Latin American Financial Markets: Developments in Financial Innovations (pp. 65-77). Ámsterdam, Holanda: Emerald Group Publishing Limited.
[8] Frankel, J. y Froot, K. (1990). “Chartists, Fundamentalists, and Trading in the Foreign Exchange Market”. The American Economic Review, 80(2), pp. 181-85.
[9] Fullerton, T.; Hattori, M. y Calderón, C. (2001). “Error Correction Exchange Rate Modeling: Evidence for Mexico”. Journal of Economics and Finance, 25(3), pp. 358-368.
[10] Gabriel, A. S. (2012). “Evaluating the Forecasting Performance of GARCH Models: Evidence from Romania”. Procedia-Social and Behavioural Sciences, 62(24), pp. 1006-1010.
[11] Jebran, K. y Iqbal, A. (2016). “Dynamics of Volatility Spillover between Stock Market and Foreign Exchange Market: Evidence from Asian Countries.” Financial Innovation, 2(3), pp. 1-20.
[12] Lim, C. M. y Sek, S. K. (2013). “Comparing the Performances of GARCH-Type Models in Capturing the Stock Market in Malaysia”. Procedia-Economics and Finance, 5(1), pp. 278-487
[13] Lorenzo, A. y Ruiz, A. (2012). “Los rendimientos cambiarios latinoamericanos y la (a) simetría de los shocks informacionales: Un análisis econométrico”. Ensayos Revista de Economía, 31(2), pp. 87-113.
[14] McKenzie, M. (2002). “The Economics of Exchange Rate Volatility Asymmetry”. International Journal of Finance and Economics, 7(3), pp. 247-260.
[15] Martínez, C. y Ramírez, M. (2011). “Dynamic Conditional Correlation in Latin American Asset Markets”. Universidad del Rosario-Facultad de Economía, Documentos de Trabajo No. 107.
[16] Maya, C. y Gómez, K. (2008). “What Exactly is ´Bad News´ in Foreign Exchange Markets? Evidence from Latin American Markets”. Cuadernos de Economía, 45(132), pp. 161-183.
[17] Nelson, D. B. (1991). “Conditional Heteroskedasticity in Asset Returns: A New Approach”. Econometrica, 59(2), pp. 347-370.
[18] Ruiz, I. (2009). “Common Volatility across Latin American Foreign Exchange Markets”. Applied Financial Economics, 19(15), pp. 1197-1211.
[19] Vitale, P. (2007). “A Guided Tour of the Market Microstructure Approach to Exchange Rate Determination”. Journal of Economic Surveys, 21(5), pp. 903-934.
[20] Zakoian, J.M. (1994). “Threshold Heteroskedastic Models”. Journal of Economic Dynamics and Control, 18(5), pp. 931-955.