RESUMEN

El objetivo de la presente investigación es identificar la relación que existe entre la desigualdad en la distribución de los ingresos y el crecimiento económico de Chile entre los años 1996 y 2017. Para ello se utilizó el Ratio de Palma y una modificación a las tradicionales mediciones del fenómeno, basándonos en las remuneraciones que perciben los trabajadores. Como hallazgo más relevante se evidenció una relación negativa entre la desigualdad y el crecimiento económico, situación compatible con la literatura que sostiene que aquellos países con mayores niveles de desigualdad tienden a crecer a una tasa menor que aquellos con mayores niveles de igualdad.

ABSTRACT

The porpouse of this investigation, is identify the relationship between the inequality in the income and the economic development growth of Chili at the period from 1996 and 2017. By this, we used the Palma´s Ratio and the modifications of the traditionals measurements of the phenomenon where we used the wages of the employees. Our result show a negative relationship between inequality and the economic growth, as show the bibilografy that hold that the countries with high level of inequality have a lower economic performance.

 

1. INTRODUCCIÓN

La desigualdad en la distribución de los ingresos ha sido uno de los problemas más difíciles de abordar para los países, situación a la que no ha estado ajena la economía chilena, la cual ha evidenciado un continuo incremento de las riquezas de un sector pequeño de la población en desmedro de la gran masa, lo que ha llevado a ser catalogada, según datos de la Organización para la Cooperación y el Desarrollo Económicos (OCDE) para el año 2015, como la segunda economía con mayor concentración del ingreso, siendo superada solamente por México¹. Esto plantea la reflexión sobre cómo puede la desigualdad en la distribución de la renta llegar a afectar al desempeño de las economías de los países.

Desde la academia, la relación entre desigualdad y crecimiento económico ha estado bajo la mirada de los investigadores durante los últimos sesenta años, como consecuencia de los planteamientos realizados por Simon Kuznets. Sobre la base de estas propuestas han sido muchos los estudios que han intentado explicar la relación que existe entre el crecimiento económico y la desigualdad, tratando no solo de identificar su dirección de causalidad, sino que también la relación que tienen en sí ambas variables. De estas investigaciones han surgido dos corrientes muy marcadas. La primera establece una relación positiva o de tipo lineal entre ambas variables, mientras que la segunda, surgida con posterioridad, sostiene que existe una relación de tipo negativa o inversa. Esta dicotomía en los planteamientos se presenta incluso en la investigación empírica, llevando a que en la actualidad no exista un consenso general en cuanto a la influencia que tienen las variables entre sí.

Para el caso de Chile no se ha desarrollado una línea investigativa sistemática que evidencie el tipo de relación entre las variables, situación que repercute directamente en la toma de decisiones y diseño de políticas que buscan disminuir la desigualdad por medio de una redistribución de la riqueza. Considerando este escenario, resulta necesario recopilar información que estime la relación entre ambas variables, de modo de poder establecer una base que sirva para la toma de decisiones de política económica que logre determinar la incidencia que tiene la desigualdad de la distribución de los ingresos y la tasa de crecimiento del PIB. En este sentido, la presente investigación busca determinar los efectos que ha causado la actual distribución de la riqueza en la tasa de crecimiento del PIB. Esto apoyado por una fuerte evidencia empírica que recorre desde la teoría clásica de la curva de Kuznets, hasta investigaciones contemporáneas, como la realizada por José Gabriel Palma. Para lograr este objetivo, en el segundo apartado de este trabajo se efectúa una revisión de la literatura internacional para establecer un marco teórico y empírico que sirva como fundamento para el desarrollo de la medición en la economía chilena, además de constituir la base del análisis de los resultados por obtener. En el tercer capítulo se abordan la metodología de evaluación y los resultados de las diferentes pruebas econométricas llevadas a cabo. Finalmente, en el cuarto apartado se desarrollan las conclusiones del estudio.

 

2. REVISIÓN DE LA LITERATURA

Explicar el crecimiento económico de los países es tema recurrente no solo en la teoría económica, sino que también en la investigación empírica, las cuales han desarrollado una gran cantidad de modelos que buscan establecer una relación causal frente a una amplia gama de variables, con la finalidad de entender cómo se genera y a partir de qué condiciones se lleva a cabo el crecimiento. Una de estas líneas de desarrollo es la que busca determinar la relación entre la desigualdad en el ingreso y el crecimiento económico. A pesar de que existe un amplio número de investigaciones referidas al tema, no se ha llegado a un consenso general acerca de la relación existente entre ambas variables; sin embargo, es posible identificar dos corrientes teóricas y empíricas que han tratado de establecer su relación a través del tiempo.

Por un lado se encuentran los autores que, basándose en los planteamientos teóricos desarrollados por Kuznets (1955), sostienen que ambas variables tienen una relación positiva. Mientras que en la otra vereda se encuentran quienes han encontrado que esta relación es de carácter negativo, argumentos que se derivan del comportamiento evidenciado en la literatura empírica al momento de estudiar el comportamiento de estas variables tanto en el continente asiático como en Latinoamérica².

Los inicios de la teoría clásica de la relación entre desigualdad y crecimiento, siendo esta la base de la corriente que sostiene la existencia de una relación positiva entre las variables, se remontan al enfoque tradicional planteado por Kuznets (1955) y su llamada hipótesis de Kuznets. En ella se muestra la existencia de un conflicto entre la igualdad y el crecimiento para aquellos países que tengan un bajo nivel de desarrollo, el que se soluciona mediante la elección de una de las dos variables como forma de llevar a cabo su política económica, en donde las autoridades han privilegiado históricamente las políticas tendientes a fomentar el crecimiento del país en desmedro de la igualdad del ingreso, lo que Okun (1975) denominó el big trade off, lo que implica sacrificar una variable con la finalidad de alcanzar la otra.

Esta hipótesis resulta ser una especie de regularidad empírica, dado a que los cambios distributivos que se producen al interior de los países se atribuyen a las diferentes etapas del crecimiento económico por el cual atraviesa. En este sentido, en etapas tempranas del crecimiento económico, la desigualdad al interior del país tenderá a crecer, para luego comenzar a disminuir conforme más desarrollado se vuelva el país, fenómeno que es planteado como un comportamiento en forma U invertida. Como forma de comprobar su hipótesis, Kuznets (1966) realizó un estudio empírico sobre nueve países industrializados, cuyos resultados demostraron un comportamiento positivo entre ambas variables en etapas tempranas de crecimiento; sin embargo, el mismo autor sugiere que sus hallazgos son de carácter tentativo, considerando que existe una limitada base de análisis.

Las razones teóricas de esta relación inicial positiva se encuentran basadas en tres supuestos (Domínguez, 2009). El Primero es que la propensión marginal al ahorro de los estratos altos de la población es mayor a la que presentan aquellos grupos sociales de menores ingresos; por lo tanto, a mayor desigualdad mayor tasa de ahorro y más rápido será el crecimiento económico³. El segundo es que los grandes proyectos de inversión requieren de altas sumas de capitales, por lo que un país al no contar con un mercado financiero desarrollado, la posibilidad de concretar estos proyectos se enfoca en unos pocos individuos de la sociedad que a su vez concentran una parte importante de la renta nacional. Y el tercero es que la desigualdad es eficiente para la economía, dado que induce a los agentes a arriesgarse y/o esforzarse más con el fin de mejorar sus niveles de bienestar relativo, lo que repercute de forma positiva en el desempeño económico de los países. En este sentido, Barro (1999) evidenció que la curva posee una regularidad empírica, hallazgos que demuestran que la desigualdad retarda el crecimiento para países pobres y lo promueve en países ricos. Sin embargo, la curva explica relativamente poco las variaciones de desigualdad entre países y a través del tiempo.

En caminos paralelos al de Kuznets hubo autores que apoyaron y reforzaron la existencia de una relación positiva entre ambas variables, para ello efectuaron una interpretación retrospectiva de la curva. En esta línea de autores se encuentran principalmente neokeynesianos, como Lewis (1954), Kaldor (1957) y Pasinetti (1962), quienes sostuvieron que la desigualdad inicial en la distribución del ingreso era necesaria para el crecimiento. Por otra parte Okun (1975) fue mucho más allá en los planteamiento, sosteniendo que la desigualdad no solo era necesaria, sino que además era buena (Domínguez 2009). Lazear y Rosen (1981) defendieron la idea de que la relación entre desigualdad y crecimiento es positiva porque la desigualdad incentiva la innovación y el espíritu empresarial, lo que a su vez promueve el crecimiento. En la misma línea, Thierry Verdier (1993) concluyó que en países con sociedades más desiguales se tiende a destinar mayores recursos financieros a educación, lo que trae consigo capital humano más capacitado y, por tanto, crecimiento.

En la misma línea de establecer la relación positiva de las variables, Robinson (1976) utilizó la hipótesis de Kuznets y la planteó como teoría de la movilidad de las personas entre el sector rural-agricultor y el urbano-industrial, sosteniendo que cada sector se caracteriza según amplitud, ingreso per cápita y desigualdad. Así, el sector rural es el más amplio, con un ingreso per cápita bajo y una desigualdad baja. El sector industrial, por su parte, es menos amplio, con un ingreso per cápita alto y una alta desigualdad. Con estos antecedentes sitúa la hipótesis como teoría considerando la movilidad y la etapa de desarrollo del país, en donde en fases tempranas, la relación entre desigualdad en el ingreso y crecimiento tiende a ser positiva, puesto que el desarrollo económico implica un movimiento de personas y recursos desde el sector rural al industrial, provocando que la población movilizada experimente un aumento de su ingreso per cápita, lo que a su vez produce un aumento de la desigualdad en la economía. En etapas tardías la relación se hace negativa, puesto que una mayor cantidad de trabajadores pobres del sector rural puede optar a unirse al sector industrial relativamente rico, explicado por la movilidad del sector en etapas tempranas. Además el arribo de nuevos trabajadores al sector industrial permite que muchos de ellos que se iniciaron en los peldaños más bajos del sector puedan ascender socialmente en relación con los trabajadores más ricos. Por último, el tamaño decreciente de la fuerza laboral del sector rural tiende a aumentar los salarios en dicho sector. En consecuencia, estas fuerzas combinadas tienden a reducir la desigualdad.

Entre los modelos más recientes basados en la curva de Kuznets se encuentra el planteado por Greenwood y Jovanovic (1990), quienes dan un realce al desarrollo del mercado financiero de un país y su cambio de un sistema no sofisticado a uno moderno como condición basal al momento de emprender políticas de crecimiento económico. Por otro lado, Helpman (1997) se enfoca en la tecnología que se encuentra disponible en el país o en los sectores económicos como causa del crecimiento, sosteniendo que el sector con menor capitalización o pobre en recursos financieros utiliza una tecnología obsoleta, mientras que el sector con mayores recursos utiliza una más avanzada.

Sin embargo, el Banco Mundial (1991) desacredita los planteamientos desarrollados en base a la curva de Kuznets de que el crecimiento económico se relaciona de manera positiva con la desigualdad, postura que asume tras contrastar la evolución que presentaron ambas variables en América Latina y el Sudeste Asiático, dando paso con ello a la creencia de que ambas variables se relacionan negativamente.

El surgimiento de esta nueva corriente teórica y empírica de la relación se da a partir de la década de 1990, donde se debate ampliamente el hecho de que la desigualdad en el ingreso sea un promovedor del crecimiento económico, planteando que la relación es de carácter negativa, sosteniendo que la desigualdad merma las posibilidades de crecimiento de los países, aun cuando la tendencia de la mayoría de los estudios se mueve hacia la validación de la hipótesis de Kuznets.

Considerando este dilema Barro (1999), esta vez buscando una forma alternativa a la explicación de la relación más allá de solo la hipótesis de Kuznets, agrupa teóricamente los estudios realizados independiente de la vertiente que siguen, esto con la finalidad de entender el modelo que subyace a la forma de pensar de cada investigador y los clasifica en cuatro categorías:

 

2.1. Imperfecciones del mercado de crédito

Según esta línea, la capacidad limitada de endeudamiento implica que las tasas de rendimiento de las oportunidades de inversión no se equiparan necesariamente al margen; por lo tanto, con un limitado acceso al crédito, la utilización de oportunidades de inversión dependerá del nivel individual de bienes e ingresos.

Lo anterior se ejemplifica para hogares pobres, quienes con un bajo nivel de ingreso tienden a renunciar a oportunidades de inversión en capital humano que ofrecen relativamente grandes tasas de retorno de la inversión. En este caso, una redistribución de bienes e ingresos de ricos a pobres tiende a aumentar la productividad promedio de las inversiones, por lo cual una reducción de la desigualdad tenderá a aumentar la tasa de crecimiento económico.

 

2.2. Política económica

Esta categoría se basa en la redistribución de recursos de ricos a pobres, favorecidos principalmente por procesos políticos que se sitúan en el poder tras un período eleccionario, en donde la población tiende a elegir gobiernos con programas económicos distributivos. Así entonces, altos grados de desigualdad tendrán como consecuencia medidas políticas orientadas a aumentar las transferencias y el gasto público. Por lo tanto, el afán redistributivo de las medidas mencionadas inhibe el esfuerzo de trabajo de la población; por ejemplo, en el caso que se grave su ingreso, creando de esta forma distorsiones dentro de la economía, que resultan en una reducción de la inversión. En consecuencia, la desigualdad afectará negativamente al crecimiento económico debido al proceso redistributivo que se lleva a cabo.

 

2.3. Disturbios sociopolíticos

Esta categoría enfatiza en que una mayor desigualdad tiende a reducir la productividad de un país. Lo anterior se explica por el aumento de la clase pobre que trae consigo complicaciones sociales que afectan el bienestar socioeconómico. Estas complicaciones derivan en un derroche de recursos del capital humano, dado que las personas prefieren interrumpir el orden social que aumentar los esfuerzos en el trabajo. En este sentido, como la población utiliza su tiempo en cosas ajenas al trabajo la productividad del país cae y, en consecuencia, también lo hará el crecimiento. Por ello, la relación entre desigualdad y crecimiento económico en este caso es negativa.

 

2.4. Tasas de ahorro

Debido al pensamiento keynesiano, algunos economistas sostienen que las tasas de ahorro individuales aumentan con el nivel de ingreso. Cumpliéndose aquello, la redistribución de ricos a pobres tendería a bajar la tasa agregada de ahorro de una economía. Por lo tanto, un aumento de la desigualdad tiende a aumentar la inversión por una mayor capitalización del dinero ahorrado, aumentando de esta forma el crecimiento económico, dándose una relación positiva entre ambas variables.

Con la nueva corriente que relaciona negativamente a las variables surgen estudios como el de Persson y Tabellini (1994), quienes realizan dos modelos de regresión con muestras históricas y actuales, evidenciando un signo negativo de la desigualdad sobre el crecimiento. Dado lo anterior, estos investigadores concluyen que la desigualdad es dañina para el crecimiento, puesto que conduce a políticas que no protegen los derechos de propiedad y no permiten la apropiación privada total de los rendimientos de la inversión. Con posterioridad Perotti (1996) crea uno de los modelos más importantes en los que evalúa la relación entre la distribución de la renta, instituciones democráticas y crecimiento a partir de distintas premisas⁴, para así plantear las hipótesis esperadas de este modelo de regresión, el cual tenía variables base de otros modelos anteriores, al que se le agregaron otras variables para probar sensibilidad⁵. A partir de lo anterior se obtiene como resultado que para cada modelo existía una relación negativa entre la desigualdad y el crecimiento. En la misma línea, del estudio de Benabou (1996) se puede desprender que el coeficiente negativo para la desigualdad del modelo, como así también en otros, es provocado en parte por factores fuera de las variables planteadas, como por ejemplo la riqueza agregada (aggregate wealth), instituciones políticas (political institutions) o el nivel de desarrollo (development level). Lo anterior reforzado por Alessina y Perotti (1996), ya que estos evidenciaron que otro de los vínculos entre la relación negativa entre desigualdad e inversión es la inestabilidad política de un país promovida por el descontento social.

En 2011 surge la investigación de Berg y Ostry, en la cual se señala que una mayor igualdad da pie para un crecimiento sostenible en el tiempo, basándose para ello en la teoría económica (Persson y Tabellini, 1994; y Easterly, 2007), la cual sostiene que a mayores niveles de desigualdad se provocan retrasos en materias de salud y educación para toda la población, lo que puede derivar en una inestabilidad social, política y económica, trayendo consigo bajas en la inversión y falta de consenso en la población para afrontar las conmociones internas o externas, traduciéndose ello en bajas en las tasas de crecimiento como también en su sustento temporal, argumento apoyado por su investigación de 2008 junto a Zettelmeyer, donde también argumentaban que un crecimiento sostenido en el tiempo se debe a instituciones más democráticas, un comercio abierto con bajas barreras de entradas y salidas y una economía sobre la base de manufactura corriente y sofisticada.

En el año 2014, Berg, Ostry y Tsangarides retomaron su investigación de 2011, esta vez evaluándola en conjunto con la variable redistribución. Con los resultados obtenidos ponen en duda lo planteado por Okun (1975), ya que en cierto grado la redistribución no tiene un efecto negativo en el crecimiento, por lo que los esfuerzos por disminuir la desigualdad sí serían útiles en pos de alcanzar un mayor crecimiento sostenible en el tiempo, lo que se llevaría a cabo mediante pequeñas transferencias destinadas a ciertas áreas, como, por ejemplo, en salud y educación.

Otros autores postulan que las investigaciones de tipo negativa no son confiables. En este sentido, Deininger y Squire (1996) advierten que muchos de los modelos estimados en donde se observa una relación negativa entre desigualdad y crecimiento no son robustas, dado que al aplicar pruebas de sensibilidad y agrupar variables explicativas adicionales o variables dummy, el coeficiente de la variable desigualdad se presenta en signo negativo pero no significativo.

En la misma línea, Li y Zou (1998), utilizando datos filtrados de la muestra de Deininger y Squire (1996), junto con los de Barro y Lee (1994) además de los de Nehru (1995) determinan que el coeficiente de regresión para la variable desigualdad medida por el Coeficiente de Gini resultó positivo. A raíz de lo anterior, concluyen que la desigualdad no es dañina para el crecimiento económico (contrario a lo que plantean Persson y Tabellini en 1994), sino que puede llevar a un incremento de este si el consumo público entra en la función de utilidad.

Por su parte, Forbes (2000) utiliza y filtra la muestra de Deininger y Squire (1996) sobre la base de tres criterios: encuestas de hogares, la población representativa y la medida del ingreso debía ser integral (incluyendo los ingresos de empleo propio, ingresos no salariales y no monetarios). El estudio arrojó como conclusión que sí cambia la evidencia empírica de investigaciones anteriores, donde el coeficiente del modelo para la desigualdad era negativo, dando paso a una relación positiva entre estas variables para el corto y mediano plazo (esto podría cambiar para países pobres). Esta relación positiva se explica por el uso mejorado de datos y el panel de estimación de control, ya que las investigaciones anteriores no utilizaban datos confiables y muchas variables exógenas permeaban al modelo, como, por ejemplo, la corrupción, que tiene relación positiva con la desigualdad y negativa con el crecimiento.

 

3. METODOLOGÍA

La investigación realizada es de tipo cuantitativa no experimental, longitudinal y correlacional, la cual abarca desde el año 1996 a 2017. La información necesaria para esta investigación fue obtenida de fuentes como el Banco Central de Chile, la Dirección de Presupuestos (Dipres) y del Instituto Nacional de Estadísticas (INE).

La correcta formulación del modelo econométrico que relaciona la desigualdad con el crecimiento económico depende, en mayor medida, del indicador de desigualdad que se utilizará. Para ello existe una gama importante de indicadores, dentro de los cuales emergen dos como principales: el Coeficiente de Gini y el Ratio o Coeficiente de Palma.

El coeficiente de Gini fue desarrollado por el estadístico y sociólogo italiano Corrado Gini (1912), y es el método de medición de la desigualdad más utilizado para estudios que abordan esta temática. Se calcula dependiendo de los datos considerados en la muestra para la medición de la desigualdad, los que pueden ser datos desagregados o datos agrupados.

En el primer caso, la metodología que se utilizará se relaciona con la curva de Lorenz y corresponde a una transformación de la fórmula inicial propuesta por Gini⁶, la cual se define de la siguiente forma:

Donde, F(y) representa la curva de Lorenz; es decir, la proporción de individuos o familias que tienen ingresos acumulados menores o iguales a y.

En el segundo caso, la fórmula de cálculo se encuentra orientada a la realización de trabajos empíricos sobre desigualdad, agrupando con ellos los datos en subconjuntos que aseguren su comparabilidad a lo largo de la muestra. Para ello, se agrupan las observaciones de forma ascendentes y en intervalos de igual tamaño (por ejemplo, deciles) y se construyen las frecuencias relativas, simple y acumulada de la variable a distribuir, así como de la población bajo estudio. Una de las fórmulas propuestas para este tipo de datos es la siguiente:

Donde, n representa el número de grupos, muestra el porcentaje de población en el grupo e el ingreso acumulado en el grupo i.

Por medio del Coeficiente de Gini se puede determinar la desigualdad en el ingreso, tomando entre 0 y 1, donde 0 corresponde a la máxima igualdad de la distribución del ingreso y 1 corresponde a la máxima desigualdad; es decir, una persona tiene el control total de los ingresos.

Por medio del Coeficiente de Gini se puede determinar la desigualdad en el ingreso, tomando entre 0 y 1, donde 0 corresponde a la máxima igualdad de la distribución del ingreso y 1 corresponde a la máxima desigualdad; es decir, una persona tiene el control total de los ingresos.

El Ratio de Palma, por su parte, surge como teoría a partir de un estudio realizado en 2011 por el economista chileno José Gabriel Palma, en el cual se determina que la desigualdad proviene de los ingresos que percibe el grupo más rico del país frente al más pobre, excluyendo a la clase media, dado que presenta un comportamiento homogéneo independiente del país bajo análisis. Posteriormente, Cobham y Summer (2013) plantearon matemáticamente el indicador utilizando los deciles 1 al 4 y 10. Así entonces, la forma de medición del indicador corresponde a la proporción de la parte más rica de la nación, medido por el decil 10, y la parte más pobre, medido por los deciles 1 al 4. Por ejemplo, que la proporción entre ambos grupos sea dos significa que la parte rica gana dos veces más que la parte pobre. En el mismo estudio, realizan una comparación entre ambos indicadores, dando a conocer algunos problemas que el Gini posee asociados principalmente a tres argumentos: a) la complejidad de cálculo del coeficiente, b) la nula característica de descomponibilidad del indicador, y c) la marcada sensibilidad ante cambios en la distribución de la clase media (50% del ingreso nacional o deciles del 5 al 9).

Considerando que ambos indicadores presentan información sobre la desigualdad, se utilizan los cinco axiomas presentados por Cobham y Summer (2013)⁷ para evaluar la mejor opción, lo que sumado a la simplicidad de visualización e interpretación del indicador, es que se optó por utilizar el coeficiente de Palma, el cual se encuentra determinado de la siguiente manera:

Sin embargo, la distribución del ingreso en Chile se mide a través de la encuesta Casen, la cual es aplicada de forma no periódica en intervalos de tiempo que abarcan los 2 o 3 años, situación que merma la disponibilidad de información para los fines del estudio. Sin embargo, Berg, Ostry y Tsangarides (2014), sostienen que la medición a través de los ingresos por remuneraciones es una mejor aproximación a la desigualdad, dado que no considera la intervención del Estado en los ingresos que sesgan los resultados de la medición. Considerando esta premisa, se utilizaron los datos provenientes de la Encuesta de Remuneraciones y Costo de la Mano de Obra del INE, la cual cuenta con información mensual del comportamiento del sueldo que perciben los trabajadores del país. No obstante, la forma de clasificación de los trabajadores se encuentra basada en las funciones que se realizan bajo la Clasificación Internacional Uniforme de Ocupaciones en su versión 88, utilizando solo 9 categorías. Como forma de unificar las clasificaciones a deciles poblacionales, se utilizó como información complementaria la Encuesta Suplementaria de Ingresos, también del INE, la cual tiene la cantidad de hogares, según decil, clasificados por grupo ocupacional. Con ese dato en específico se puede establecer el porcentaje de participación de los grupos ocupacionales en los deciles.

Por ejemplo, para 2009 un 51% de los ocupados del grupo ocupacional Personal Directivo se encontraba en el decil 10. Así también del grupo ocupacional Profesionales, con un 43%. Esto indica que el decil 10 está compuesto, en su mayoría, por ambos grupos, situación que se replicó para los siete grupos restantes (ver tablas n.° 9 y n.° 10 en los anexos). Mediante esta metodología, se clasificó cada grupo ocupacional según decil, estableciendo que el decil 10 está compuesto por los grupos Personal Directivo y Profesionales. Por su parte, los deciles del 1 al 4 están compuestos por los grupos Trabajadores de Servicios Personales y Protección, Empleados de Comercio y Demostración, Operadores de Maquinarias e Instalaciones y Trabajadores no Calificados. En consecuencia, la nueva forma de medir el Coeficiente de Palma está dado por:

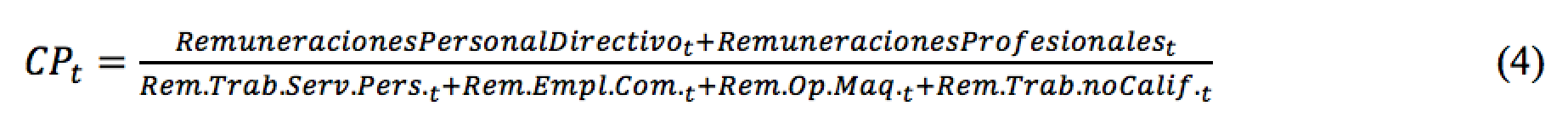
Como forma de obtener una base de datos de 85 observaciones fue necesario expandir la variable desigualdad, la cual no presenta valores informados por el INE a partir de enero de 2010, mediante la siguiente forma:

Para el resto de variables no fue necesaria una expansión de las observaciones Sin embargo, para determinar el PIB per cápita se dividió el valor del PIB trimestral entregado por el Banco Central de Chile por la cantidad de personas ocupadas en el país según el Instituto Nacional de Estadísticas.

El modelo econométrico considerado para el estudio se realiza bajo el método de mínimos cuadrados ordinarios (MCO), por lo que se espera que el resultado obtenido sea consistente con los cuatro supuestos básicos de una regresión lineal. No obstante, algunos de estos supuestos se pueden obviar en pro de los resultados obtenidos, considerando que la finalidad de la investigación es identificar el tipo de relación que entre ellas existe para distintos períodos y no generar un modelo predictivo entre la tasa de crecimiento del PIB (TcPIB) y la desigualdad, quedando un modelo determinado de la siguiente forma:

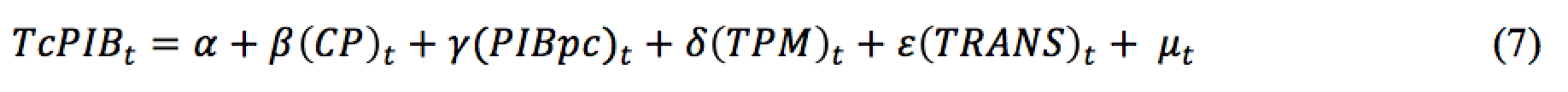
Donde:

: PIB per cápita de la masa laboral ocupada.

TPM: tasa de política monetaria.

TRANS: transferencias corrientes.

Como forma de facilitar la interpretación de los resultados, se procedió a efectuar una transformación logarítmica de las variables, las cuales fueron sometidas a los test de raíz unitaria de Dickey-Fuller y de estacionalidad a través de un análisis de gráficos lineales.

Tabla 1. Cuadro resumen test Raíz Unitaria y Estacionalidad

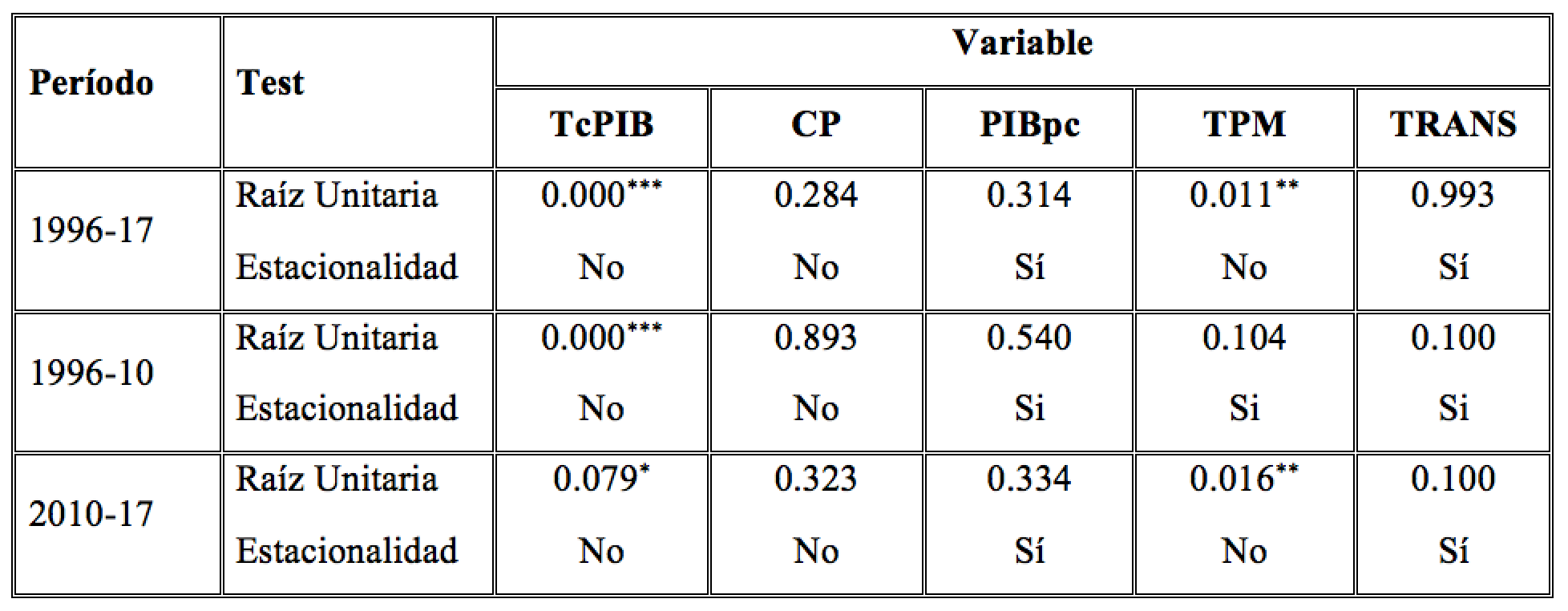
Nivel de significancia: *0.1; **0.05; ***0.01.

      Fuente: elaboración propia sobre la base de resultados de EViews.

Para aquellas variables que presentaron problemas de no estacionariedad, se les aplicó un ajuste a través de la aplicación del Filtro de Hodrick-Prescott (HP), que extrae el ciclo y tendencia de la serie. Para las series que presentaron ambos comportamientos se realizó, en primera instancia, un ajuste estacional a través de aplicación del Census X-12, que extrae la estacionalidad de la serie, para posteriormente aplicar el filtro HP quedando el modelo especificado de la siguiente forma:

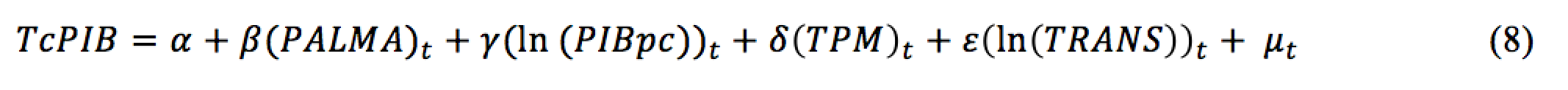
En la estimación del modelo se llevó a cabo una prueba global del período entre el segundo trimestre de 1996 y el segundo trimestre de 2017, seguido de pruebas de sensibilidad y omisión de variables con la finalidad de comprobar la robustez y la confiabilidad de la medición (ver Tabla 2).

Tabla 2. Resultados modelos de mínimos cuadrados entre 1996 y 2017

Nivel de significancia: *0.1; **0.05; ***0.01.

    Fuente: elaboración propia sobre la base de resultados de EViews.

Los siguientes modelos se construyen con la base de datos reducida, buscando con ello evidenciar dos períodos temporales distintos (ver Tabla 3). Con el primero se quiere analizar un período de homogeneidad y estabilidad, tomando en consideración una tendencia política uniforme. Para ello, se utilizará como muestra la etapa correspondiente a los gobiernos de centro-izquierda. Con el segundo, se intenta analizar un intervalo temporal que contenga diferentes matices políticos, por lo que se toma los años entre 2010 y 2017 debido a la transición política evidenciada en este período.

Tabla 3. Resultados modelos entre 1996 y 2010

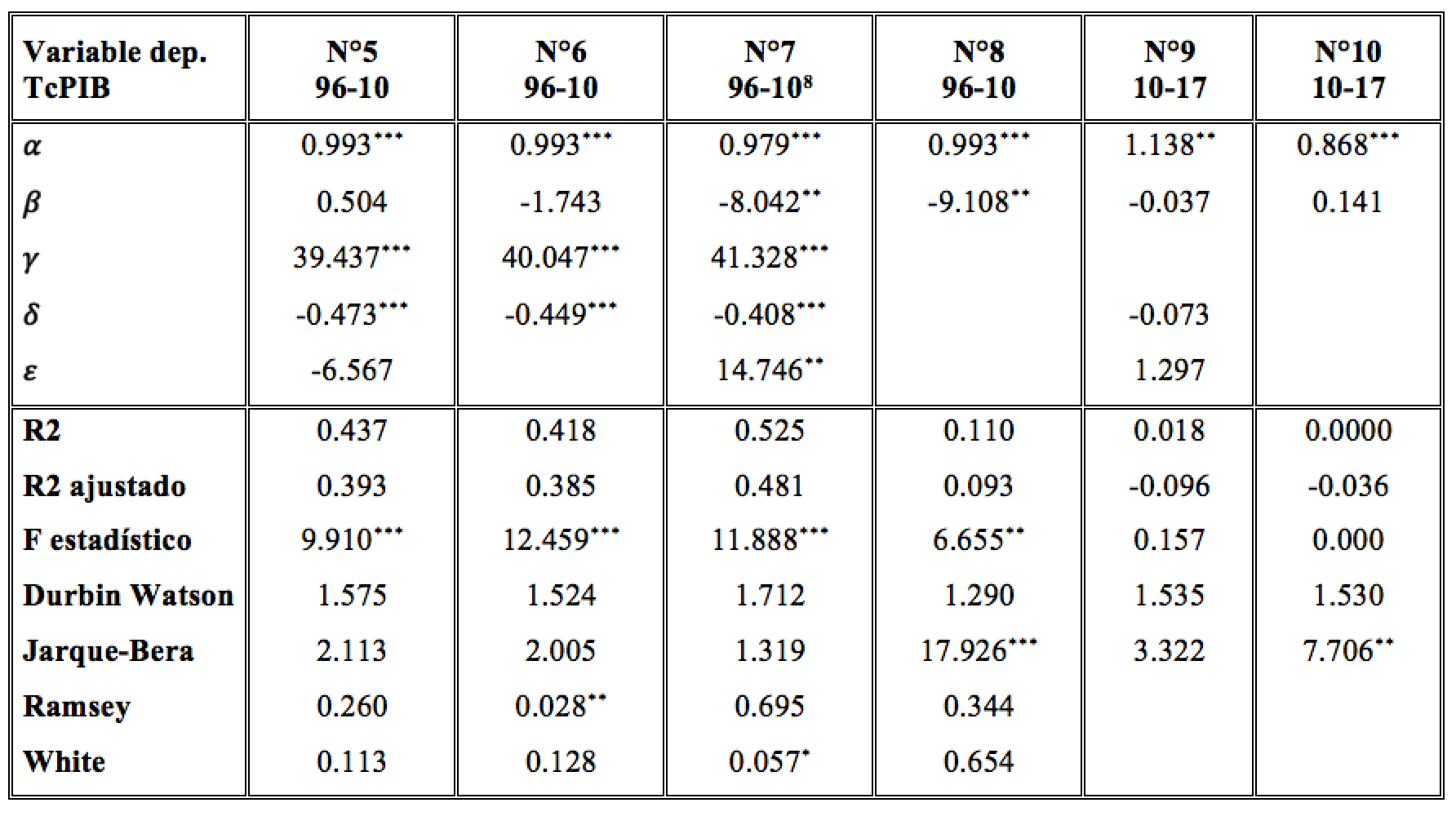
Nivel de significancia: *0.1; **0.05; ***0.01.

Fuente: elaboración propia sobre la base de resultados de EViews.

Respecto del período de concertación, el primer modelo evidencia que las variables CP y TRANS son no significativas, teniendo además signo contrario al esperado en sus coeficientes; por lo cual, se procedió a eliminar la variable TRANS para estimar un segundo modelo. En este se puede observar que la serie CP continúa siendo no significativa; sin embargo, posee la relación negativa esperada con la tasa de crecimiento del PIB. Ahora bien, el tercer modelo nace a partir de la idea de evidenciar si las políticas de gobierno respecto de las remuneraciones y transferencias afectan a la tasa de crecimiento del PIB de manera tardía. Para ello se aplicaron rezagos a las series CP y TRANS, buscando con esto validar este fenómeno⁸. Las variables CP y TRANS son significativas al 5%, mientras que el PIBpc y la TPM son significativas al 1%, mientras que los signos obtenidos para cada variable fueron los esperados, además tener normalidad de los residuos y homocedasticidad e independencia de los errores. En el modelo n.° 4 se lleva a cabo una nueva estimación que busca ver la incidencia directa de la serie CP en la variable dependiente, en donde la variable independiente es significativa al 5% y con signo esperado, con un r ajustado es cercano al 10%, por lo que explica en gran medida a la variable TcPIB.

Respecto de los modelos n.° 9 y n.° 10, se puede observar que no hay significancia en la variable CP. Dado este resultado, y a pesar que posee signo de coeficiente esperado, se descarta la aplicación de pruebas para evaluar los supuestos básicos.

La idea de realizar nuevos modelos con la serie CP como variable dependiente surge por los resultados obtenidos tras realizar la prueba VIF a la totalidad de los modelos de modo de evaluar la multicolinealidad de las variables, y los resultados muestran que ninguna de ellas presenta una dependencia entre sí (ver Tabla 4).

Tabla 4. Resumen de test VIF para evaluar multicolinealidad

Fuente: elaboración propia sobre la base de resultados de EViews.

De la Tabla 4 se puede verificar que cada vez que se incorpora u omite la serie TRANS en un modelo, se ve afectado en gran medida el VIF que presenta la variable CP; es por ello que se llevaron a cabo modelos en donde se utilizó esta última como dependiente, resultados que se muestran en la tabla 5.

Tabla 5. Resumen modelos con la serie CP como variable dependiente

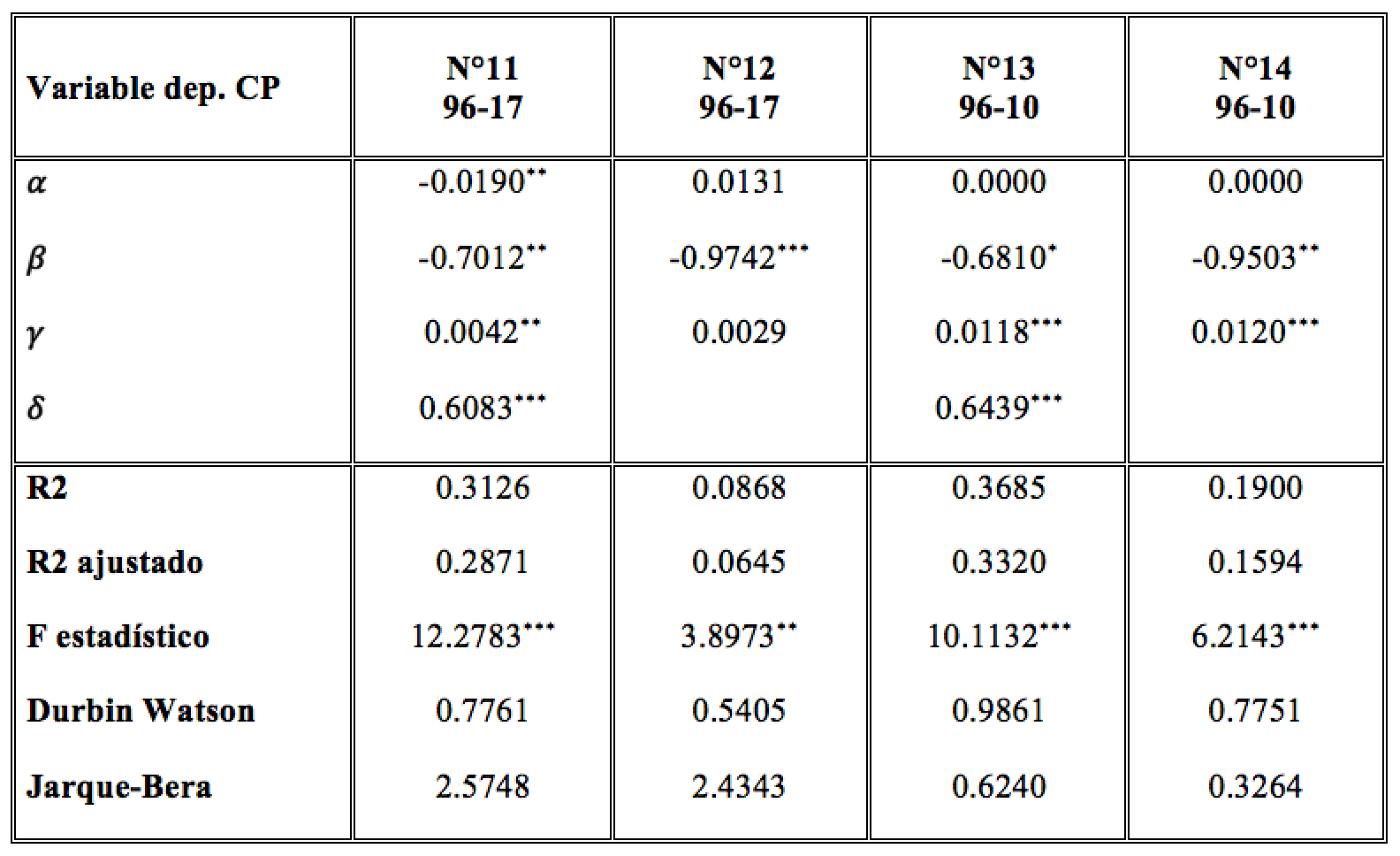
Nivel de significancia: *0.1; **0.05; ***0.01

          Fuente: elaboración propia sobre la base de resultados de EViews.

De la Tabla 5 se puede evidenciar que para los dos períodos expuestos el omitir la variable TRANS genera que el r ajustado de los modelos n.° 12 y n.° 14 disminuya. Por lo tanto, se observa que existe evidencia preliminar de que la variable TRANS causa ciertos problemas de multicolinealidad. Como forma de determinar la relación causal entre las variables, se llevó a cabo una prueba de Granger, cuyos resultados muestran la relación causal entre la desigualdad y las transferencias corrientes que efectúa el Estado (ver Tabla 6).

Tabla 6. Test de causalidad

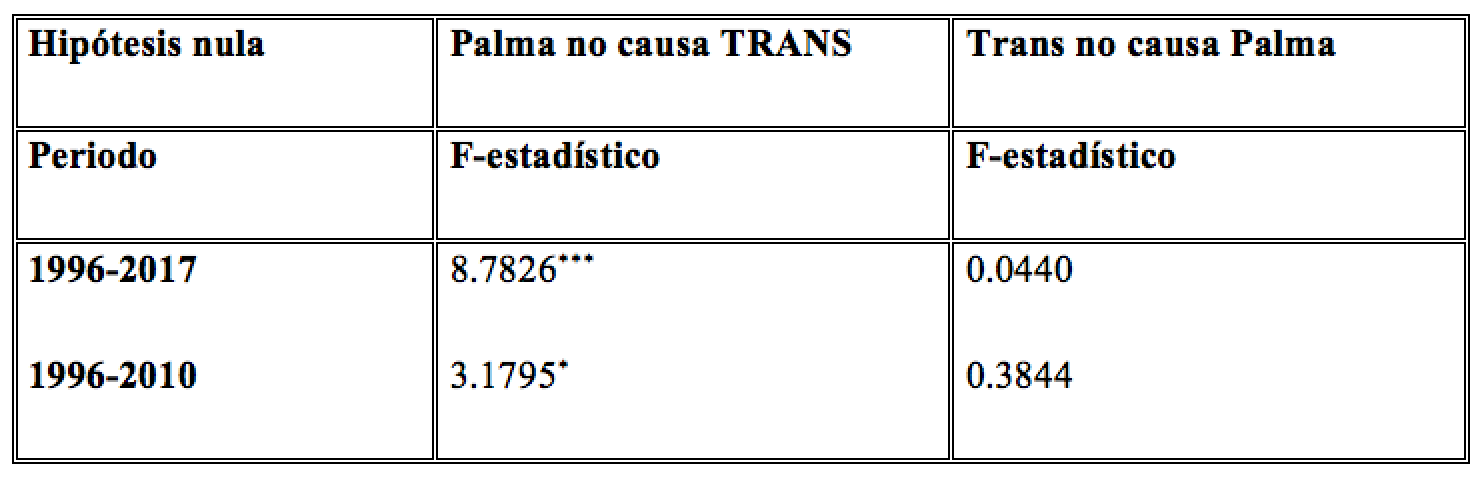
Nivel de significancia: *0.1; **0.05; ***0.01

Fuente: elaboración propia sobre la base de resultados de EViews.

 

4. CONCLUSIONES

De esta investigación se concluye, principalmente, que la desigualdad remuneracional, medida bajo la metodología de Palma, afecta significativa y negativamente al crecimiento económico. A raíz de este hallazgo es factible mencionar que se cumple con el objetivo central de este estudio y se valida la hipótesis en él presentado.

Respecto de la variable desigualdad, que se midió por la relación entre el ingreso salarial del 10% más rico y el 40% más pobre, existe suficiente evidencia empírica como para mencionar que sí se puede utilizar como estimador de la desigualdad en Chile. No obstante, por sí sola no explica la desigualdad total en el país.

Para las variables desigualdad y tasa de política monetaria, el signo evidenciado en el coeficiente se condice con la teoría económica (Persson y Tabellini 1994; Perotti 1996; Verdier 1993; Alesina y Rodrik 1994; Berg y Ostry 2011; Easterly, 2007), siendo en ambos casos negativo en relación con la tasa de crecimiento del PIB. Con esto se cumple con las hipótesis de relación inversa planteadas al inicio de la investigación.

Para las variables PIB per cápita de los ocupados y transferencias corrientes, el signo evidenciado en el coeficiente se condice con la teoría económica (Berg, Ostry y Tsangarides, 2014), siendo en ambos casos positivo en relación con la tasa de crecimiento del PIB. Con esto se cumple con las hipótesis de relación directa planteadas al inicio de la investigación.

Ahora bien, considerando dos de los periodos estudiados, que van desde el segundo trimestre de 1996 al segundo trimestre de 2017 y del segundo trimestre de 1996 al primer trimestre de 2010, se encontraron signos claros de que la desigualdad remuneracional para estos contextos influye de manera importante a la tasa de crecimiento del PIB, explicando en un 10% la primera variable mencionada a la segunda en ambos períodos. Sin embargo, los hallazgos evidencian que aquello no se presenta como tal en intervalos temporales acotados y con múltiples transiciones políticas, tal como se evidenció en el modelo n.° 10. Estos lapsos crean una inestabilidad de la serie que no permite la correcta estimación de la relación entre desigualdad y tasa de crecimiento del PIB, lo que obliga a tener una base de datos más representativa, situación que no se da en la historia política abarcada en la muestra.

Respecto de las transferencias corrientes, los resultados fueron bastante representativos en evidenciar que ella afecta de forma negativa tanto en el presente como en el pasado (rezagos), aun cuando esta variable tiene relación directa y significativa con la tasa de crecimiento del PIB.

Sin embargo, el resultado más concluyente se obtiene al realizar la prueba de causalidad. En ella se evidencia de forma notoria que la desigualdad causa directamente a las transferencias, no dándose aquello en sentido contrario. Lo anterior concuerda con lo que la teoría económica específica sobre ambas variables, dado que un país con más desigualdad tiende a la redistribución desde ricos hacia pobres. Por tanto, agregar las transferencias al modelo supone un aumento en el grado de multicolinealidad y explicación de la variable desigualdad sobre la tasa de crecimiento del PIB. La evidencia anterior no es lo suficientemente fuerte como para rechazar el modelo, pero sí entrega señales claras para tener presentes en este tipo de situaciones.

Considerando lo anterior, es posible afirmar que el trabajo de investigación se alinea a estudios anteriores respecto del área económica analizada.

 

REFERENCIAS BIBLIOGRÁFICAS

Alesina, A. y Perotti, R. (1996). Income Distribution, Political Instability, and Investment. European Economic Review, 40(6),1203-1228.

Alesina, A. y Rodrik, D. (1994). Redistributive Politics and Economic Growth. Quarterly Journal of Economics, 109(2), 465-490.

Banco Mundial (1991). Informe sobre el Desarrollo Mundial 1991: la tarea acuciante del desarrollo. Washington, D.C.

Barro, R. y Lee, J. (1994). Source of Economic Growth. Carnegie-Rochester Conference Series on Policy,40(1), 1-46.

Barro, R. (1999). Inequality, Growth, and Investment. NBER Working Paper, 7038.

Barro, R. (1999). Inequality and growth in a panel of countries. Journal of Economic growth, 5(1), 5-32.

Bénabou, R. (1996). Inequality and Growth. NBER Working Paper, 5658.

Berg, A. y Ostry, J. (2011). Inequality and unsustainable growth: Two sides of the same coin? Washington. Recuperado de https://www.imf.org/external/pubs/ft/sdn/2011 /sdn1108.pdf. Consultado el 5 de abril de 2018.

Berg, A., Ostry, J. y Zettelmeyer, J. (2008). What makes growth sustained? Journal of Development Economics, 98(2), 149-166.

Berg, A., Ostry, J. y Tsangarides, Ch. (2014). Redistribution, Inequality and Growth. Washington. Recuperado de https://www.imf.org/external/pubs/ft/sdn/2014/ sdn1402.pdf. Consultado el 5 de abril de 2018.

Cobham, A. y Summer, A. (2013). Is It All About the Tails? The Palma Measure of Income Inequality. Washington. Recuperado de https://www.cgdev.org/sites/default/files/it-all-about-tails-palma-measure-income-inequality.pdf. Consultado el 4 de mayo de 2018.

Deininger, K. y Squire, L. (1996). A New Data Set Measuring Income Inequality. The World Bank Economic Review, 10(3), 565-591.

Domínguez Martín, R. (2009). Desigualdad y bloqueo al desarrollo en América Latina. Universidad de Cantabria. Recuperado de http://www.ciberoamericana.com/pdf/ DesigualdadBloqueo.pdf. Consultado el 4 de mayo de 2018.

Easterly, W. (2007). Inequality Does Cause Underdevelopment: Insights from a New Instrument. Journal of Development Economics, 84(2), 755-776.

Forbes, K. (2000). A reassessment of the relationship between inequality and growth. The american economic review, 90(4), 869-887.

Greenwood, J. y Jonavic, B. (1990). Financial Development, Growth, and the Distribution of Income. The Journal of Political Economy, 98(5), 1076-1107.

Helpman, E. (1997). General Purpose Technologies and Economic Growth. Cambridge MA. Recuperado de https://mitpress.mit.edu/books/general-purpose-technologies-and-economic-growth. Consultado el 15 de mayo de 2018.

Kaldor, N. (1957). A model of economic growth. The Economic Journal, 67(268), 591-624.

Kuznets, S. (1955). Economic growth and income inequality. The American economic review, 45(1), 1-28

Kuznets, S. (1966). Modern Economic Growth. Yale University Press.

Lazear, E. y Rosen, Sh. (1981). Rank-Order Tournaments as Optimum Labor Contracts. Journal of Political Economy, 89(5), 841-864.

Lewis, A. (1954). Economic Development with Unlimited Supplies of Labor. The Manchester School, 22(2), 139-191.

Li, H. y Zou, H. (1998). Income inequality is not harmful for growth: theory and evidence. Review of Development Economics, 2(3), 318–334.

Nehru, V., Swanson, E. y Dubey, A. (1995). A New Database on Human Capital Stock in Developing and Industrial Countries: Sources, Methodology, and Results. Journal of Development Economics, 46(2), 379-401.

Okun, A. (1975). Equality and efficiency: The big trade-off. Primera edición. Washington, Estados Unidos: Brookings Institution Press,.

Palma, J. (2011). Homogeneous Middles vs. Heterogeneous Tails, and the End of the ‘Inverted-U’: It’s All About the Share of the Rich. Development and change, 42, 87-153.

Pasinetti, L. (1962). Rate of Profit and Income Distribution in Relation to the Rate of Economic Growth. The Review of Economic Studies, 29(4), 267-279.

Perotti, R. (1993). Political Equilibrium, Income Distribution and Growth. Review of Economic Studies, 60(4), 755-776.

Perotti, R. (1996). Growth, Income Distribution and Democracy: What the Data Say. Journal of Economic Growth, 1(2), 149-187.

Persson, T. y Tabellini, G. (1994). Is Inequality Harmful for Growth? American Economic Review, 84(3), 600-621.

Robinson, Sh. (1976). A note on the U-hypothesis relating income inequality and economic development. American Economic Review. 66, 437-440.

Saint-Paul, G. y Thierry, V. (1993). Education, Democracy and Growth. Journal of Development Economics, 42(2), 399-407.

1. Información extraída desde el Centro para las Oportunidades e Igualdad de la OCDE.
2. Las diferencias mencionadas corresponden al nivel de desarrollo alcanzado por ambos continentes, considerando condiciones similares en un comienzo del proceso. Esto es, la discordancia entre ellos ante mismas condiciones económicas, pero distintos niveles de desigualdad (diferencias en el nivel de ingreso per cápita y educativo, entre otras). Mientras en el continente asiático la desigualdad era baja, lo que permitió un desarrollo mayor, en Latinoamérica la desigualdad era elevada, situación que inhibió el proceso de desarrollo.
3. Este supuesto proviene de la idea de Kaldor, Kalecki y Pasinetti y su visión de que los beneficios financian la inversión. De esta forma, un sistema bancario que genere crédito con fluidez es esencial para el crecimiento, puesto que genera fuertes incentivos a la inversión. De los beneficios obtenidos por ella surge el ahorro que financia, a su vez, la inversión realizada. Sin embargo, este proceso es llevado a cabo en su mayoría por la clase más adinerada de cada nación, quienes ahorran marginalmente más que los pobres y, por tanto, aumenta la desigualdad en conjunto con un rápido crecimiento económico.
4. Premisas sobre la base de la Política Fiscal, Inestabilidad Sociopolítica, Imperfecciones de Mercado y Disposición al Ahorro. Para más información véase Perotti (1996).
5. Estas variables fueron GR (tasa de crecimiento per cápita de GDP), GDP, MSE (escolaridad promedio masculina), MSF (escolaridad promedio femenina), PPPI (valor PPP sobre la base del deflactor inversión) y MID (participación en el ingreso del quinto y cuarto quintil).
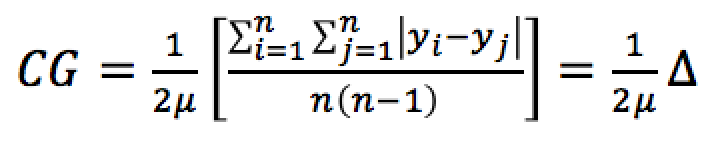6. , donde representa la media aritmética de las n(n-1) diferencias absolutas de las observaciones y es el valor máximo que asume cuando un individuo concentra todo el ingreso.
7. Los axiomas son: Atkinson, señal de la política, claridad, respuesta política y horizontal.
8.   La razón de aplicar este método solo para el período entre 1996 y 2010 es que la tendencia política presente en este es una misma. No así para los períodos van desde 1996 a 2017 y 2010 a 2017. Considerando aquello, se puede pensar que el efecto tardío de políticas estatales se puede ver mermado por las diferencias ideológicas en los dos últimos lapsos mencionados.